Несколько интересных задач на логику.
Все задачи взяты отсюда. Спасибо, хабрахабр.
Не торопитесь открывать ответ. Подумайте над решением :-D
Задачи замечательно подходят как просто для размышлений, так и для проведения олимпиады.
Задача 1: Парадокс лжеца (куда без нее?). Она очень простенькая, как многие, конечно, знают. Но пост про задачи без нее был бы неполон.
Условие
Вы долго шли по дороге и вот вы, наконец, пришли к вашей цели. Перед вами две двери. И вы точно знаете, что за одной сокровище, которые вы так долго искали, а за другой длительная и мучительная смерть. Перед дверью сидят два человека. Вы точно знаете, что один из них всегда говорит правду, а другой всегда лжет. Вы также точно знаете, что они оба точно знают за какой дверью что. И также они точно знают кто из них кто. И, конечно, они оба уверены, что пришли вы сюда именно за сокровищем.
Вопрос:
Какой один вопрос задать и кому, чтобы открыть наверняка правильную дверь?
[spoiler effect=”slide” show=”Показать ответ” hide=”Закрыть”]Ответ: “Какую дверь мне скажет открыть другой из вас двоих?”
Изначально понятно, что нет разницы кого из двоих спрашивать. Мы подходим к любому и задаем вопрос из ответа. Рассмотрим два варианта:
— Если так вышло, что мы подошли к лжецу, то он подумает, что другой скажет правильную дверь и укажет вам на другую, так как он всегда лжет. В результате вы получите неправильную дверь.
— если так вышло, что мы подошли к правдивому человеку, то он также укажет вам на неправильную дверь, так как он вам правдиво скажет, что другой соврет.
В результате, кого бы мы не спросили, мы получит указание на неправильную дверь. Нам остается только открыть другую и наслаждаться сокровищами.[/spoiler]
Задача 2: В оригинале “Togglers”. Назовем их “Перебежчики”. Несколько расширенная задачка про лжецов.
Условие
Перед нами пять человек. Из них четверо — “перебежчики”. Кто такие эти “перебежчики”? Все очень просто. Если любому из них, независимо от других задавать вопросы, то с каждым следующим, он будут менять свои ответы с лживых на правдивые и наоборот.
Мы не знаем в каком “настроении” они находятся изначально. Но точно знаем, что если они один раз ответили правду, то в следующий раз соврут, и наоборот — если первый раз соврали, то потом обязательно скажут правду.
Но один из этих пяти не “перебежчик”. Он всегда говорит правду.
Вопрос:
Как найти этого пятого, который всегда говорит правду, если можно всего два вопроса, причём каждый только кому-то одному?
Вопрос можно задавать, как и в прошлой задаче, кому угодно из них. Оба вопроса задаем одному и тому же человеку.
“Ты всегда говоришь правду?”
Дальше:
— если мы получили ответ “Да”, то следующий наш вопрос будет “Кто всегда говорит правду?”
— если мы получили ответ “Нет”, то следующий наш вопрос будет “Кто „перебежчик“?”
Решение:
После первого вопроса мы можем получить ответы “Да” и “Нет”. Рассмотрим что это нам дает:
— “Да” означает, что или мы попали на человека, который всегда говорит правду, или мы попали на врущего “перебежчика”. Таким образом следующий ответ будет точно правдивым, а значит если мы спросим “Кто всегда говорит правду?” нам укажут на правильного человека.
— “Нет” означает, что мы попали на правдивого “перебежчика”. А это значит, что он точно соврет в следующий раз. Значит на наш вопрос: “Кто „перебежчик“?”, ему придется указать нам на единственного не “перебежчика” среди этой замечательной пятерки.
[/spoiler]
Задача 3: Про ящики с табличками
Условие
Перед нами три ящика с яблоками, грушами и в третьем есть и яблоки и груши. На всех ящиках есть замечательные таблички: “Яблоки”, “Груши”, “Яблоки и Груши”.
Но вот беда: таблички перепутались, и как это водится, в ящиках темно, ничего не видно, и мы можем только просунуть руку в дырку и достать что нибудь из ящика.
Вопрос: Какое найменьшее количество фруктов нужно достать и откуда, чтобы развесить таблички снова правильно, если мы знаем, что на всех ящиках теперь висят неправильные таблички.
[spoiler effect=”slide” show=”Показать ответ” hide=”Закрыть”]
Ответ:
Достаточно достать один фрукт из ящика, на котором табличка “Яблоки и Груши”
Решение:
Так как мы знаем, что таблички неверны, то в этом ящике или яблоки или груши. Допустим нам попалось яблоко. Тогда мы снимаем табличку “Яблоки” с того ящика, на котором она висит и вешаем ее вместо таблички “Яблоки и Груши”. Теперь у нас остался ящик, на котором красуется неправильная табличка “Груши” и у нас в руках табличка “Яблоки и Груши”. Теперь переломный момент. Как разобраться куда вешать что? Очень просто. Используем условие, что мы знает, что ВСЕ таблички висят неправильно, а значит перевешиваем табличку “Груши” на ящик, на котором в самом начале было написано “Яблоки”, потому что эта табличка никак не может остаться на своем месте. И вешаем табличку “Яблоки и Груши” на единственное свободное место.
Задача 4: Про торт и бесстыдную птичку
Условие
У бабушки было два внука, которые должны были приехать на выходные погостить. Она, как любая добропорядочная бабушка, приготовила для них торт (очень вкусный). И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые части.
Бабушка имеет идеальный глазомер, она легко способна находить на глаз середины и пересечения любых отрезков. И у бабушки есть замечательный нож (из немецкой стали), которым она умеет лихо отрезать куски торта по любой намеченной прямой.
Вопрос:
Какое минимальное количество разрезов нужно сделать бабушке, чтобы разрезать торт?
(Уточнение, это именно торт, не пирог. Его нельзя разрезать по горизонтали, так как тогда одному из внуков придется довольствоваться только кремом)
После вырезания куска торт, схематически выглядит так:
Ответ
Все линии проходящие через центр прямоугольника делят его площадь точно пополам.
Условие
Десять заключенных завтра поставят на лестницу так, что каждый будет смотреть в спину тому, кто стоит ниже. Таким образом он будет видить всех, кто стоит перед ним. На них на всех оденут шапки. Шапки будут или черными или белыми. Само собой цвет своей шапки никто из них не будет видеть. Шапки будут распределены произвольно — могут быть все черные, могут все белые, а могут вперемешку. Это будут решать смотрители тюрьмы прямо на месте.
Далее смотрители идут сверху лестницы вниз и спрашивают у каждого: “Какого цвета твоя шапка?”. Если он отвечает правильно, его отпускают на волю. Если ошибается — убивают.
Вопрос:
У заключенных есть целая ночь, чтобы придумать стратегию поведения. Помогите им гарантировано спасти так много людей, как это только возможно.
Заключенные должны выбрать какой нибудь цвет. Пусть это будет черный. Тогда верхний заключенный, номер 10, должен посчитать шапки черного цвета. Далее он должен сказать “черный” если шапок черного цвета было четное количество, и “белый”, если шапок черного цвета было нечетное количество. Его жизнь, конечно же, не гарантирована. Ему может повезти, а может не повезти.
Тот заключенный, что под ним, номер 9, должен сравнить то, что видит он с тем, что сказал предыдущий. Допустим, первый сказал “черный”. Далее есть два варианта:
— номер 9 видит четное количество черных шапок. Тогда он говорит “белый”, потому, что количество черных шапок осталось тем же, а значит на нем белая. Это дает номеру 8 информацию о том, что черных шапок осталось четное количество.
— номер 9 видит нечетное количество черных шапок. Это означает, что он сам под черной шапкой. Тогда он говорит “черный” и номер 8 понимает, что теперь черных шапок нечетное количество.
И так далее. Таким образом мы гарантированно спасли целых девять закаленных тюрьмой человеческих жизней.
Условие
В пещере живут 100 гномиков. Однажды Белоснежке, которая, конечно, живет с ними, стало скучно и она связала всем гномикам разноцветные шапочки, которые они с удовольствием носят. Конечно же они, при этом не знают какого цвета шапка одета на них, так как одевала их Белоснежка в кромешной темноте.
Причем, гномики — существа довольно апатичные. Все, чем они занимаются в пещере — это сидят в кругу и смотрят друг на друга. Они даже не разговаривают и вообще никакой социальной жизни не ведут. Просто сидят, смотрят и о чем-то думают. Каждый гномик видит остальных 99 гномиков. Соответственно, каждый видит все шапки у всех гномиков, кроме своей. Каждый день, Белоснежка, чтобы не потерять любимых гномиков выводит их на построение перед пещерой. И каждый раз она говорит им: “Кто в голубой шапке — выйти из строя”. Гномики, которые уверены на 100%, что на них голубая шапка после этого сделают шаг вперед. Если гномик считает, что его шапка может быть иного цвета, он останется стоять как вкопанный. Чтобы избежать замешательства добавим факт, что те гномики, которые из строя таки вышли переводятся в другую пещеру. Судить о том, что кого-то не хватает остальные гномики могут только когда вернутся в свою пещеру и сядут на свои места в кругу.
Вопрос:
Что будет происходить на построении, на какой день и почему, если мы знаем такие три вещи:
— Белоснежка, со скуки, надела на всех гномиков голубые шапочки.
— Белоснежка сказала гномикам, что есть хотя бы один гномик в голубой шапочке.
— Гномики, за многие годы жизни в пещере, отточили свою логику до совершенства. Она непогрешима. И каждый из них понимает, что у всех остальных гномиков такая же непогрешимая логика.
99 дней не будет происходить ничего, на сотый все гномики сделают шаг вперед.
Решение:
Он сидит в комнате целый день и никого не видит. Так как он знает, что должен быть хотя бы один гномик в голубой шапочке, то на первом же построении он сделает шаг вперед, так как будет на 100% уверен в цвете своей шапочки.
Теперь рассмотрим вариант, когда гномика два. Они целый день сидят в пещере и смотрят друг на друга. Что они видят?
Они видят, что напротив сидит гномик в голубой шапочке. Теперь они не уверены в цвете своей шапочки, так как они знают, что должен быть хотя бы один гномик в голубой шапочке и как раз его они перед собой и видят. Но что бы было, если бы один из них увидел на другом не голубую шапочку, а, скажем, красную? Это привело бы его к логике с предыдущего шага, там где у нас был один гномик. А значит он вышел бы на первом же построении.
Когда же гномики видят, что этого не произошло и они оба остались стоять как вкопанные на построении (так как в нашем случае оба видят по голубой шапочке напротив себя), каждый из них сразу понимает, зная, что у каждого гномика непогрешимая логика, что, если бы другой гномик не увидел бы голубой шапочки на нем самом, то тот гномик вышел бы на первом же построении вперед. Факт того, что этого не произошло, достаточен, чтобы оба гномика стали уверенными в цвете своей шапки и, потому они выйдут на вместе на второй день.
Эта же логика легко расширяется на произвольное количество гномиков.
Условие
В двух одинаковых бокалах налито одинаковое количество разной жидкости. В одном — вино, в другом — вода (в этой задаче будем считать, что в вине воды нет).
Мы набираем полную чайную ложку вина из бокала, собственно, с вином и выливаем в воду. Тщательно перемешиваем и зачерпнув ту же полную чайную ложку того, что вышло, переливаем это назад в бокал с вином.
Вопрос:
Чего в чем больше — воды в вине или вина в воде?
Одинаково
Решение:
бокал 1: 6 единиц вина
бокал 2: 8 единиц воды + 2 единицы вина
После перемешивания, мы забираем чайную ложку того, что получилось из бокала 2. В этой ложке пропорции жидкостей такие же как и в самом бокале. А именно:
воды: 0.8 * 2 = 1.6
вина: 0.2 * 2 = 0.4
После переливания этой чайной ложки назад в бокал с вином:
бокал 1: 6.4 единиц вина + 1.6 единиц воды
бокал 2: 6.4 единиц воды + 1.6 единиц вина
Задача 8: Про ряд из лампочек. (за задачку спасибо nullbie)
Условие
В ряд стоят 100 лампочек.
Возле каждой есть кнопка, которая переключает состояние лампочки на противоположное, то есть, если лампочка была включена, то после нажатия на кнопку, будет выключена. И наоборот.
Мимо лампочек пускают шеренгу из ста людей. Первый нажимает на кнопку каждой лампочки, второй — на кнопку каждой второй, третий — на кнопку каждой третьей и тд.
Вопрос:
Какие лампочки будут гореть после прохода этих 100 человек, если изначально все были выключены.
1 4 9 16 25 36 49 64 81 100
Решение:
8 = 1 * 8
8 = 2 * 4
То есть в этом случае, для лампочки с номером 8 – первый человек ее включит, второй выключит, четвертый снова включит и восьмой выключит.
Единственные числа с нечетным количеством делителей — полные квадраты, например 9:
9 = 1 * 9
9 = 3 * 3
Таким образом, у числа 9 есть 3 разных делителя, а значит лампочка с этим номером останется гореть. Аналогично для всех остальных полных квадратов.
Задача 9: Задача про площади.
Условие
[spoiler effect=”slide” show=”Показать ответ” hide=”Закрыть”]
Ответ:
28
Решение:
Проведем прямую EF, которая будет параллельна прямым AB и CD (точка D внизу, она случайно обрезалась). Теперь, если будем двигать точку О в точку Т (пересечение зеленых прямых), то площадь треугольников не поменяется. Дальше все просто. Если кто придумает другое решение — я буду рад его услышать, потому что мое выглядит немного как костыль. Прошу прощения за качества рисунка, под рукой только телефон.
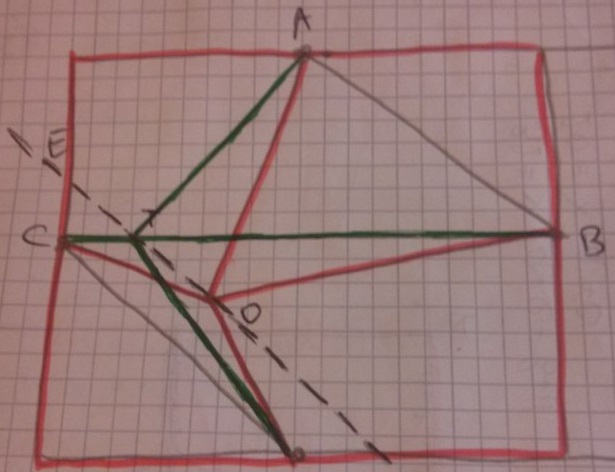
Решение 2
Решение 2: Спасибо за него Xitsa
Проведём дополнительные линии из точки в углы. После этого уже существующие станут медианами треугольников. Как известно, медиана делит площадь треугольника пополам:
Отсюда уравнения:
a+d=32
a+b=20
b+c=16
И легко получаем c+d= 32+16-20=28
Решение 3
Решение 3: За него спасибо oleg1977
пусть 2а — сторона квадрата, из O опускаем высоты х, у, (2а-х) и (2а-у).
Дальше система уравнений (площади 4-угольников из площадей 3-угольников):
ax/2 + ay/2 = 20,
ay/2 + a(2a-x)/2 = 16
ax/2 + a(2a-y)/2 = 32ax/2 -a(2a-x)/2 = 4
ay/2 -a(2a-y)/2 = -12
ax/2 + ay/2 = 20ax = a^2 + 4
ay = a^2 — 12
a^2 + 2 — 6 = 20Искомое: а(2а-х)/2 + а(2а-у)/2 = 2а^2 — ax/2 — ay/2 = a^2 — 2 + 6 = 24 — 2 + 6 = 28
Задача 10: Заключенные и лампочка
Условие
В тюрьме сидят 100 заключенных. Надзирателям захотелось, как всегда, поразвлекаться и они придумали следующую “игру”. Заключенных собираются в произвольном порядке с произвольной частотой водить в комнату, где есть только лампочка и выключатель к ней. Надзиратели также выбирают одного из заключенных (ответственный заключенный), которого при каждом приходе в камеру с лампочкой спрашивают все ли из этих 100 заключенных побывали в камере. Он может сказать, что он не уверен сколько угодно раз. Но, если он говорит, что, мол, да, все побывали, то происходит следующее. Если он не ошибся — всех отпускают, а если ошибся, то, как водится, казнят.
Вопрос:
У заключенных есть ночь, чтобы придумать хитрый план как спастись. Помогите им с разработкой их стратегии. Изначально лампочка выключена.
[spoiler effect=”slide” show=”Показать ответ” hide=”Закрыть”]
Ответ и решение:
Заключенные должны договориться, что тот, кого выберут ответственным за всех, должен всегда включать лампочку, когда заходит в комнату с ней. Все же остальные должны ее выключать, но прикасаться к ней только один раз. То есть если заключенный 1 один раз выключил лампочку, то больше он ее не трогает, в каком бы состоянии ее не обнаружил, когда зайдет в комнату. Ответственный заключенный должен считать количество раз, которые ему пришлось включить лампочку. Как только набралось 100 он может с уверенностью сказать, что все заключенные побывали в комнате.
[/spoiler]
Задача 11: Задачка про фокусника и карты. (уже не помню где взял, но решал, когда 4 часа сидел в очереди за новым свидетельством о рождении. Не решил :)
Условие
Фокусник берет стандартную колоду из 52 карт, и отдает ее зрителям. Зрители выбирают (каким угодно способом) любые 5 карт и отдают их помощнику фокусника. Тот смотрит на карты и называет фокуснику 4 из них. В ответ фокусник называет пятую. Кроме мастей и значений карт, фокусник не получает никакой дополнительной информации (помощник говорит ровным голосом, без пауз и т.д.).Вопрос:
Каким образом фокуснику удается “угадать” пятую карту?
Помощник получил от зрителей 5 карт. По скольку мастей карт всего 4, значит по крайней мере 2 карты имеют одинаковую масть. Эту масть и будет угадывать фокусник. Первая карта которую назовет помощник будет иметь ту же масть, что и карта которую надо будет угадать фокуснику(помощник в праве сам выбрать какую карту не называть). С мастью разобрались. Чтобы узнать тип карты, работает знаменитая система двоичного исчисления. Поскольку разных карт в колоде всего 13, а помощник будет называть 4 карты при этом 4 карты это 4 бита, то с помощью 4 бит можно изобразить максимальное число 1111, что в десятичной системе 1*2^3+1*2 ^2+1*2^1+1*2^0=1*8+1*4+1*2+1=8+4+2+1=15, то есть вполне достаточно для изображения 13 карт. Пусть 2=2,3=3,4=4…10=10, валет=11, дама=12, король=13, туз=14. Теперь для обозначения “1” карта называется так “сначала масть, потом сама карта”, для обозначения “0” — “сначала карта потом масть”.
И напоследок для настроения,
Задача 12: Про смотрящую корову (детская)
Условие
Знакомьтесь, это корова. Она смотрит.
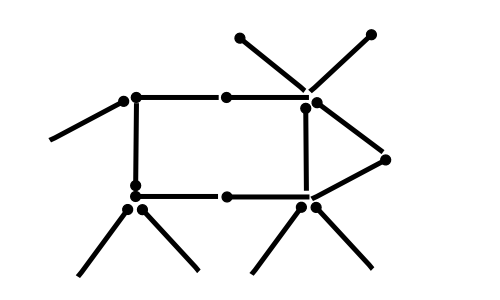
Вопрос:
Как, переложив 2 спички, можно заставить корову смотреть в другую сторону?
Ответ и решение
[spoiler effect=”slide” show=”Показать ответ” hide=”Закрыть”]
Ответ:
[/spoiler]
Большое спасибо за внимание! Надеюсь вы увидите здесь что нибудь новое для себя.